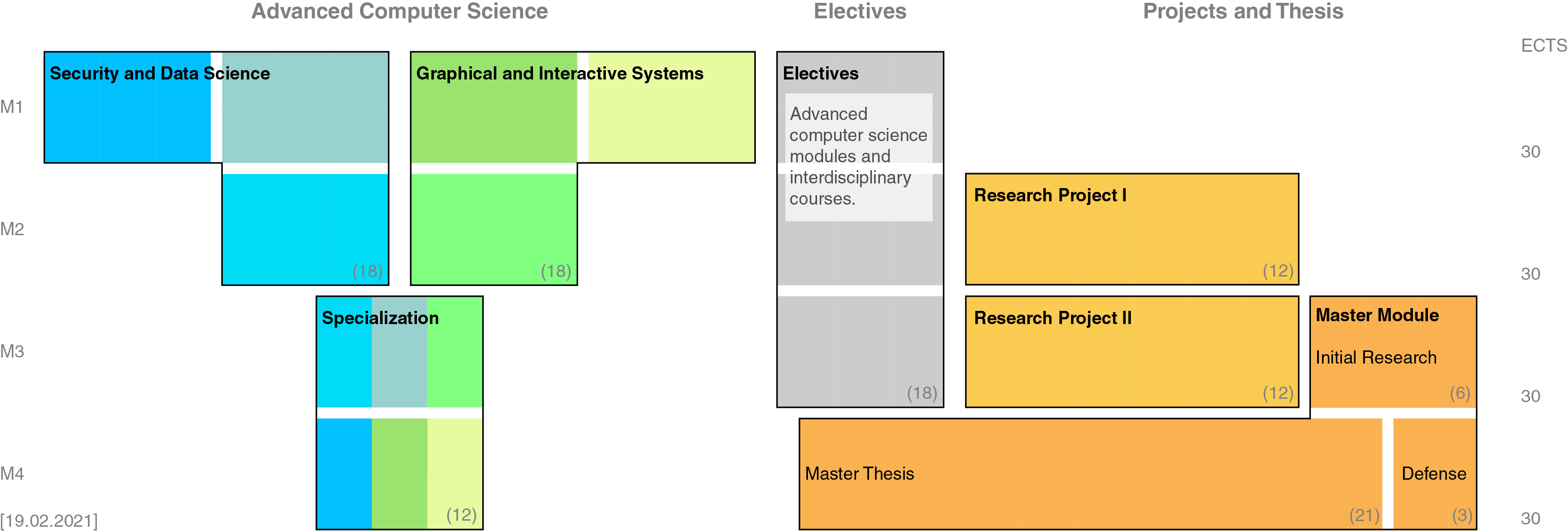
Courses | Security and Data Science | Graphical & Interactive Systems | Electives | Specialization | |
Advanced Analysis |
| x | x | ||
Advanced Cryptography: Cryptographic Hash Functions | x | x | x | Prerequisite: Cryptography introductory course | |
Advanced Cryptography: Secure Channels | x | x | x | Prerequisite: Cryptography introductory course | |
Advanced Numerical Mathematics | x | x | x | ||
Advanced Type Theory for Functional Programming |
| x | x | ||
Complexity Theory | x | x | x | ||
Computer Graphics II: Animation Systems |
| x | x | x | |
Computer Graphics II: Fundamentals of Imaging |
| x | x | x | |
Digital Watermarking & Steganography | x | x | x | ||
Discrete Optimization | x | x | x | ||
Geometry |
| x | x | ||
HCI Theory and Methods |
| x | x | x | |
Image Analysis and Object Recognition |
| x | x | x | |
Introduction to Functional Programming with Haskell |
| x | x | ||
Introduction to Machine Learning and Data Mining | x | x | x | ||
Introduction to Modern Cryptography | x | x | x | Bach.course open for Masters who had no Crypto | |
Introduction to Natural Language Processing | x | x | x | ||
Logics and Semantic Web | x | x | x | ||
Machine Learning for Software Eng. | x | x | x | ||
Online Computation | x | x | x | ||
Photogrammetric Computer Vision |
| x | x | x | |
Physiological Computing |
| x | x | x | |
Quantum Algorithms & Cryptanalysis | x | x | x | ||
Randomized Algorithms | x | x | x | ||
Search Algorithms | x | x | x | ||
Security Engineering | x | x | x | ||
Software Product Line Engineering | x | x | x | ||
Spatial Computational Geometry |
| x | x | x | |
Spatial Information Systems (GIS) |
| x | x | x | |
Ubiquitous Computing |
| x | x | x | |
Usability Engineering |
| x | x | x | |
Virtual Reality |
| x | x | x | |
Visualization |
| x | x | x | Bach.course open for Masters who had no Visualization |
Web Search and Information Retrieval | x |
| x | x |
Complete Module Catalogue of the Computer Science for Digital Media Master's program (summer semester 2017 to summer semester 2020)
Courses | Modelling | Distributed and Secure Systems | Intelligent Information Systems | Graphical & Interactive Systems | Specialization |
Advanced Analysis | • | • | |||
| Advanced Cryptography: Cryptographic Hash Functions | • | • | |||
| Advanced Cryptography: Secure Channels | • | • | |||
| Advanced HCI: Ubiquitous Computing | • | • | |||
Advanced HCI: Theory and Methods | • | ||||
Advanced Numerical Mathematics | • | • | |||
Advanced Type Theory for Functional Programming | • | • | |||
Cognitive Systems | • | ||||
Computer Graphics II: Animation Systems | • | • | |||
Computer Graphics II: Fundamentals of Imaging | • | • | |||
Discrete Optimization | • | • | |||
Geometry | • | • | |||
Image Analysis and Object Recognition | • | ||||
Internet der Dinge | (Elective only) |
|
|
|
|
Introduction to Functional Programming with Haskell | • | • | |||
Introduction to Machine Learning and Data Mining | • | • | |||
Logics and Semantic Web | • | • | |||
Machine Learning for Software Engineering | • | • | |||
Mobile Information Systems |
| • | |||
Online Computation | • | • | |||
Photogrammetric Computer Vision | • | ||||
Physiological Computing |
|
|
| • |
|
| Quantum Algorithms & Cryptanalysis | • | • | |||
Randomized Algorithms | • | • | |||
Safety and Security Engineering | • | • | |||
Search Algorithms | • | • | |||
Search-Based Software Engineering | • | • | |||
Security Engineering (replaces Software Development for Save and Secure Systems) |
| • |
|
| • |
Software Product Line Engineering | • | • | |||
Spatial Computational Geometry | • | • | |||
Spatial Information Systems (GIS) | (Elective only) | ||||
Usability Engineering | • | ||||
Virtual Reality | • | ||||
Visualization | (Elective only) | ||||
Watermarking & Steganography | • * | • | • | ||
Web Search and Information Retrieval | • | • |
* (by application to the examination committee)