"The Dynamics Of Opinion Exchange"
Masterarbeit, Sven Banisch
ISCTE - Instituto Universitário de Lisboa und Bauhaus-Universität Weimar, Dezember 2009![]()
Kontakt: http://www.lampeauftisch.de/UniVerseCity.html
Abstract:
Opinion Dynamics refers to opinion and attitude research using mathematical and physical tools. In this thesis, such a mathematical model of opinion exchange dynamics is developed. Systematic computations as well as analytical arguments are used in the model analysis, and the empirical relevance of the results is discussed using real data.
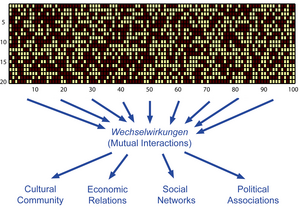
The model is based on an abstract representation of opinions as a series of k bits representing different issues in the agents mind. After an initial set--up, an iteration process is performed through which similarity leads to interaction and interaction leads to still more similarity. Individuals interact if the difference in the opinion strings is below a similarity threshold dI . Depending on dI , different behaviour of the population is observed: low values result in a configuration of highly fragmented opinions and higher values yield global consensus.
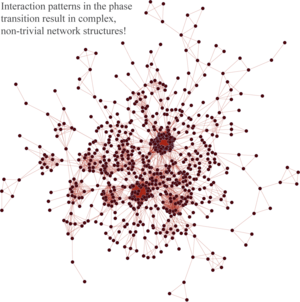
The first contribution of this research is to identify the values of parameters dI and k, such that the transition between fragmented opinions and homogeneity takes place. Systematic numerical experiments are used for this purpose. Then, we look at the transition from two perspectives: first by studying the group size distribution and second by analysing the communication network that is formed by the interactions that take place during the simulation. The emerging networks are classified by statistical means and we find that non--trivial social structures emerge from simple rules for individual communication. This emphasises the crucial role played by mutual interactions among individuals with diverse opinions and attitudes in the formation of society (as thought, for instance, by G. Simmel).
The second part of this thesis explores by analytical means the dynamical process that leads to polarisation, plurality or homogeneity. Considering sets of configurations of the agent population with an equal distribution of opinions as the states of a discrete system allows to define a Markov chain corresponding to the interaction process of the model. This is started with the simplest case of binary opinions where states are either 'yes' or 'no'. Considering the case in which individuals can choose between three opinions shows that the introduction of a confidence threshold (i.e., dI ) leads to the creation of new final states. Opinion clustering is thus the result of agents with bounded confidence. It is shown that the Markov chain machinery can be applied to the more general cases also. The method provides an analytical explanation of the convergence behaviour of this and other opinion models.
The main deficit of previous computer--aided opinion studies is that they lack a comparison to real data. To overcome this, some new ideas for a closer link of opinion dynamics models and reality are presented. The endogenous generation of interaction networks allows to link model outcomes to a series of recent network studies. Important structural properties are reproduced by the model. Then, an artificial election process is performed on the transient opinion profiles and the results are compared to real election data. Remarkable statistical agreement with the empirical data is found. We also show that the model assumptions are well--grounded in the socio--psychological understanding of human individual action.
In general, this thesis shows that computational studies are enriched essentially if analytical arguments are provided in addition, and that (no matter the tools that are used in the analysis) a comparison to empirical data greatly increases the scientific value of models.