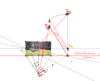
Perspektive eines Kubus im Wald
edit ~ 0 kommentare/fragen ~ 10. Dez 2019 14:25
Einige Tips für die Konstruktion:
Fotos die als Hintergrund für eine Perspektive dienen sollen sollten waagerecht und ohne Verkippung fotografiert werden. Dann geht der Horizont als waagerechte Linie durch die Bildmitte. Der halbe Öffnungswinkel der Kamera wird am unteren Bildrand angetragen und ergibt im Schnitt mit dem Lot aus der Bildmitte das Auge im Lageplan.
Konnte man aus dem Bild die Fluchtpunkte des Kubus ermitteln, sollten man diese vom Horizont auf die Bildebene im Lageplan (in der Regel der untere Bildrand) herunterloten. Der Thaleskreis um den Mittelpunkt der Strecke zwischen FL und FR durch die beiden Fluchtpunkte schneidet ebenfalls das Auge im Lot unter der Bildmitte.
Entweder gibt es Referenzkanten im Foto, von denen man ausgehen kann und oder der Öffnungswinkel des Kamerobjektives ist bekannt (Landscape oder Portrait). Dieser läßt sich messen, indem zwei Linien vom Objektiv aus so gezeichnet werden, daß sie gerade noch an den Sucherkanten (links und rechts) sichtbar sind. Der Winkel zwischen den Kanten wird mit dem Winkelmesser gemessen.
Sind keine "gebauten" Kanten im Foto zu sehen, sollte wenigstens die Lage des vordersten Punktes des Würfels im Foto bekannt sein und der Verdrehwinkel der Würfelhauptfassade zur Fotografierrichtung (Bildmittelpunkt (HP)).
Dieser liegt bei waagerechtem Geländeverlauf im Durchschnitt 1.75m unter dem Horizont des Bildes. Bei ansteigendem oder abfallendem Gelände sollte der Höhenunterschied zwischen dem nahesten Würfelpunkt und dem Fußpunkt des Fotografen bekannt sein und entsprechend berücksichtigt werden.
Aus der im Bild gemessenen Augenhöhe eines Menschen (1.75m) läßt sich jedes erforderliche Höhenmaß dorch direkte Proportionalität ermitteln.
Zur Ermittlung der richtig verkürzten Würfelfassaden helfen die Fluchtpunkte der Fassadendiagonalen. Sie sind in einer Schnittansicht jeweils unter 45° nach oben oder unten auf der geschnittenen Bildebene zu finder und müssen senkrecht über bzw. unter FL bzw FR angetragen werden.
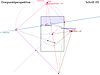
Perspektive mit drei Fluchtpunkten
edit ~ 0 kommentare/fragen ~ 6. Dez 2019 14:00
Liebe Studentinnen und Studenten des ersten Semesters,
Nach Axonometrie und Normalperspektive mit waagerechtem Blick folgt unter diesem link die Beschreibung einer Perspektivekonstruktion mit geneigtem Blick. Alle Elemente der Konstruktion ergeben sich aus einer Bildidee, die bestimmt wird durch: Lage und Neigung des Horizontes, Position des des Hauptpunktes und Lage und Neigung einer Referenzkante des Entwurfes (hier eine Kubusgrundkante).
In folgenden Schritten kann man die Konstruktion nachvollziehen:
Schritt 01 Ausgangslage
Schritt 02 Auge in Seitenansicht
Schritt 03 unterer Fluchtpunkt und linke Fluchtgerade
Schritt 04 rechter Fluchtpunkt und rechte Fluchtgerade
Schritt 05 Grundrissuntersicht und Diagonalenfluchtpunkt
Schritt 06 Würfelgrundfläche
Schritt 07 untere Sichtpyramidenseiten (grün und magenta) und rechter Diagonalenfluchtpunkt
Schritt 08 Vordere Würfelseiten
Schritt 09 Würfeldeckfläche
Schritt 10 Fertige Konstruktion
Die Konstruktionen sind mit der freien Software Geogebra hergestellt. Die Punkte A und B sowie ein Punkt am Horizont sind beweglich (bitte langsam).
Die Konstruktion der Dreipunktperspektive erschließt sich schnell, wenn man sie als dreieckige Pyramide betrachtet, deren Spitze das Auge ist, ihre Höhe die Distanz und ihre Grundfläche durch die drei Fluchtpunkte Fl Fr und Fu gegeben ist. Da die Pyramidenseiten rechtwinklige Dreiecke sind, kann msn sie mit Hilfe der Thaleskreise an den Grundkanten der Pyramide ganz einfach in die Ebene des Bildes legen. So lassen sich von den drei in die Bildebene gelegten Augpunkten alle notwendigen Fluchtpunkte bestimmen.
Die Dateien 3PP8.exe (Win) und 3PP8.zip (Mac) sind Tutorials, die zeigen wie eine Dreipunktperspektive aus dem Grundriss konstruiert wird. Ich habe sie mit Adobe Director gemacht.