IFD:EAI SoS21/course material/Session 3: File Structuring, Pointers and Addresses: Difference between revisions
From Medien Wiki
| Line 11: | Line 11: | ||
To get the x- and y-coordinates in our code, we can use the private variables for point p1 (_x and _y) and the member functions getX() and getY() for point p2. So the most crucial lines of code are: | To get the x- and y-coordinates in our code, we can use the private variables for point p1 (_x and _y) and the member functions getX() and getY() for point p2. So the most crucial lines of code are: | ||
<source lang="c++" line start="1" highlight="4">float Point2D::calculateDistanceToOtherPoint(Point2D p2){ | <source lang="c++" line start="1" highlight="4">float Point2D::calculateDistanceToOtherPoint(Point2D p2){ | ||
float distance = sqrt( (p2.getX() -_x)*( p2.getX() -_x)+( p2.getY()-_y)*( p2.getY() -_y) ); | float distance = sqrt( (p2.getX() -_x)*( p2.getX() -_x)+( p2.getY()-_y)*( p2.getY() -_y) ); | ||
return distance; | return distance; | ||
Revision as of 15:08, 26 April 2021
Homework/Recap from Session 2:
Here are the solutions of last week's task. Please try a little to solve on your own, before you peek in here! :)
Distance Function Complete Code
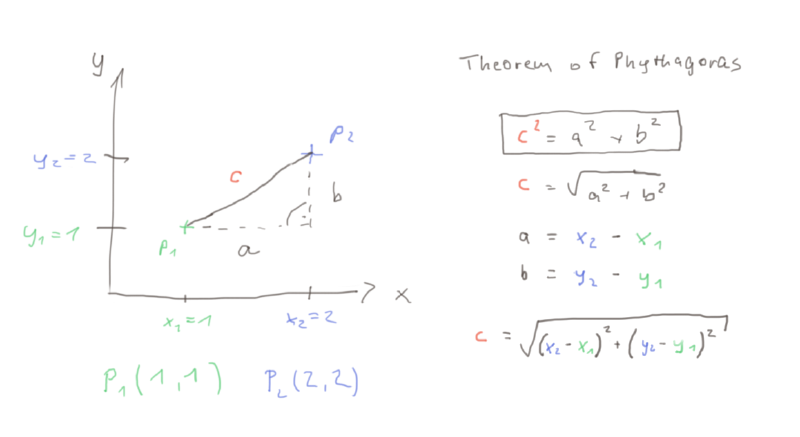
To get the distance between two points on a 2D plane we can use the Pythagorean theorem as depicted in the picture below. We give coordinates to the points and use the coordinates to calculate the distance according to the formula c = sqrt( (x2-x1)^2 + (y2-y1)^2 ), where c is the distance between the two points.
To get the x- and y-coordinates in our code, we can use the private variables for point p1 (_x and _y) and the member functions getX() and getY() for point p2. So the most crucial lines of code are:
float Point2D::calculateDistanceToOtherPoint(Point2D p2){
float distance = sqrt( (p2.getX() -_x)*( p2.getX() -_x)+( p2.getY()-_y)*( p2.getY() -_y) );
return distance;
}