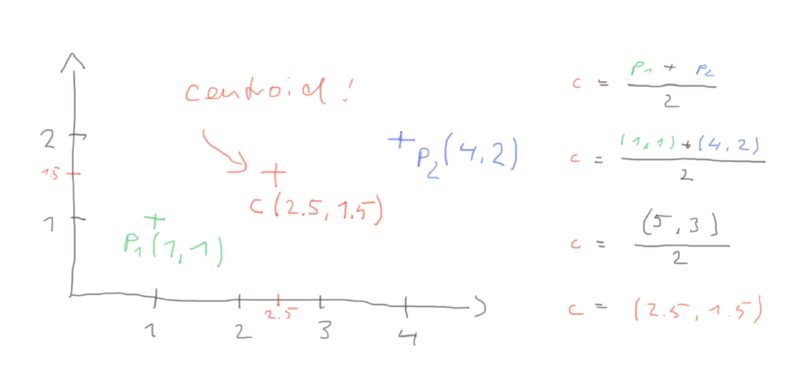Homework/Recap from Session 2:

Here are the solutions of last week's task. Please try a little to solve on your own, before you peek in here! :)

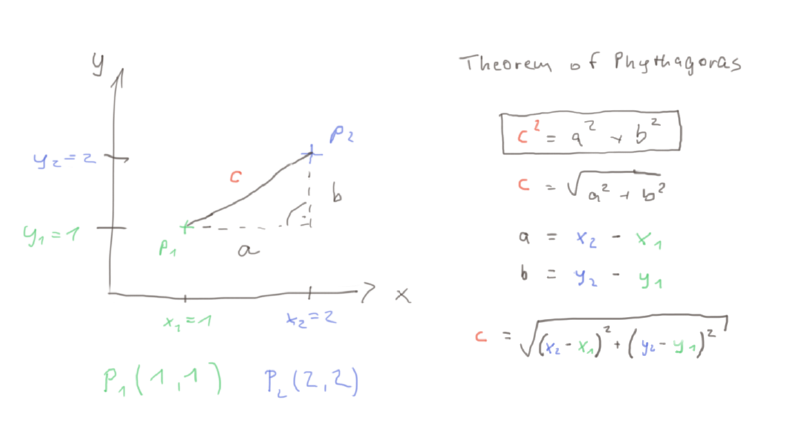
To get the distance between two points on a 2D plane we can use the Pythagorean theorem as depicted in the picture below. We give coordinates to the points and use the coordinates to calculate the distance according to the formula c = sqrt( (x2-x1)^2 + (y2-y1)^2 ), where c is the distance between the two points.

To get the x- and y-coordinates in our code, we can use the private variables for point p1 (_x and _y) and the member functions getX() and getY() for point p2. So the most crucial lines of code are:

float Point2D::calculateDistanceToOtherPoint(Point2D p2){
    float distance = sqrt( (p2.getX() -_x)*( p2.getX() -_x)+( p2.getY()-_y)*( p2.getY() -_y) ); 
    return distance;
}

Note that, for the sqrt() function to be known to the compiler, you need to include the math library with

#include <math.h>

Distance Function Complete Code

Session 3: File Structuring, Preprocessor, Compiler & Linker

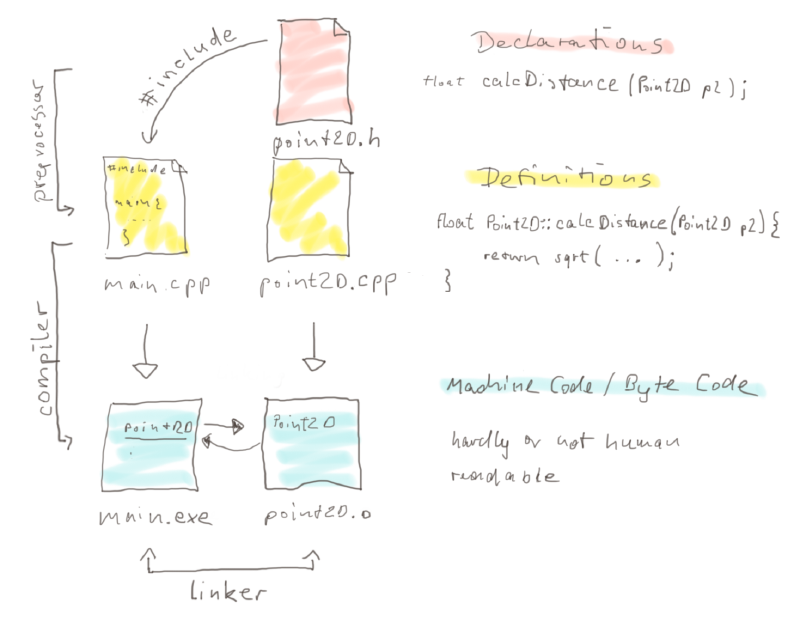
To make good use of C++, we need to structure our code in header files (.h) and source files (.cpp). The idea is, that every source file acts like a wheel in our machinery, that does only one thing and can be reused in other spots of our code to solve the same problem, if it must.

Furthermore, by structering our code in nice little modules, the compiler has less work to do, since it only needs to compile the modules that we work on and that we changed. Note that only the source files get explicitly compiled! The headers are directly copied into the source files by the preprocessor and act as an index to point to the other source files as depicted below.

Think of the headers as a table of contents that helps the programmers and the compiler and linker to know where the functions in the source files reside.

Pointers and Addresses

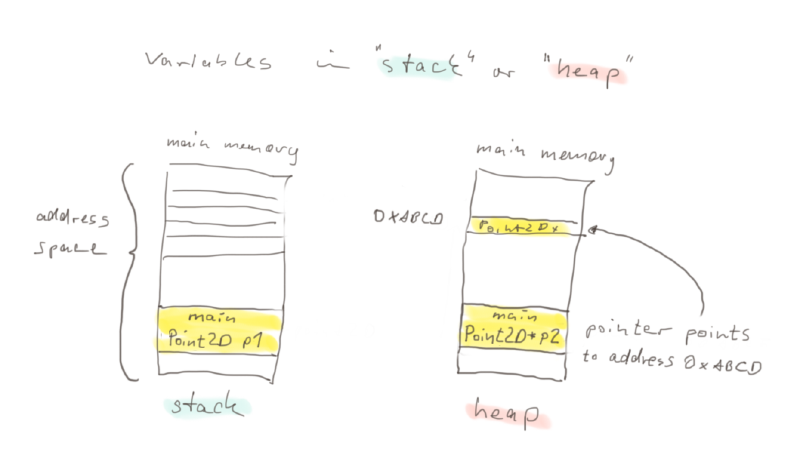
Until now, we were only using variables in a very local space in the main memory, called the stack. The stack is a very compact structure where most of the variables and program code usually reside. It's called "stack" because the variables really stack up there, on after the other, depending of the order you instantiate them. The syntax for creating a Point2D as a stack variable is as follows:

Point2D p1 = Point2D(1,2);

If we use pointers however we can use memory space everywhere in the main memory. This space is used by other programs as well and rather loosely organized. This is why it is called "heap". When we create a pointer to our Point2D, the syntax is like this:

Point2D* p2 = new Point2D(1,2);
...
delete p2;

We need to use the asterisk to denote, that we want to create a pointer and we need to use the "new" keyword to reserve the memory for our Point2D. After the "new" keyword we can initialize our Point2D directly as shown before. Note that p2 resides in the memory, when we do not delete it explicitly. Usually until you restart your computer!

Code Example for Pointers and Addresses

Homework Task

This week's task is related to machine learning. You will code the foundation of a classifier: the calculation of the centroid of a point cloud.

A short explanation: We will implement the k-means clustering algorithm for sound objects. This clustering algorithm can find data points that are close to each other and are thus considered to be the same "class" of sounds. In a machine learning context a point typically consists of measurements of multiple features of a real world object. This can be e.g. the physical dimension, the color, the weight, etc. When two real world objects are similar, then typically their taken measurements are similar, too. This means, when you consider two objects as two points on a 2D plane, then, if these objects are similar, their corresponding points on the 2D plane are close to each other. In our case, we will measure the spectral intensity of different sounds and our classifier will group sounds in accordance to their spectral intensities. Thus, spectrally bright sounds can be separated from sprectrally dull sounds. Depending of what features we present the classifier as our fundamental data, we can discern much more characteristics in our input sounds, e.g. the speed of the attack, or even the fundamental pitch, or the harmonics in our sounds.

The centroid is the center point of such a cluster of points of similar sounds and is very important for a clustering algorithm to decide to which cluster a data point belongs.

To calculate a centroid of a collection of points (our cluster) we need to do two steps:

sum up our points:

p0 + p1 + p2 + p3 ... = sum

divide the sum by out number of point:

centroid = sum / num_of_points

Example Centroid Calculation

Note: We sum up points simply by adding up their x and y values. E.g.

  p0 = (1,1),  p1= (4,2)
  c = p0 + p1;
  c = (1,1) + (4,2) = (5,3)

Dividing the point by a number, means to divide both dimensions by the same number:

  centroid = p2 /3 = (5,3) / 2 = (2.5,1.5)

In this case our centroid is (2.5,1.5). As you can see from the drawing above, the centroid lies exactly in the middle of our two points.

Programming Task

Extend our Point2D class to have the following functions:

 Point2D operator+(Point2D& p2);

This function should add up two points and return a new Point2D, which is the sum of the two points. If you implement this function you can then simply write: Point2D sum = p0 + p1; (where p0 and p1 are of the class Point2D)

 Point2D operator/(float f);

This function should divide a point by the number f and return a new Point2D which is the divided point. If you implement this function you can then simply write:

 Point2D div = p0 / 5;

(where p0 is of class Point2D)

Write an algorithm that calculates the centroid of the given points!
Use a for loop to add up any given number of points! (for this, put the points into an array and then access the array in the loop!)

If you are curious of the operator+ and operator/ statements, google "cpp operator overloading" !

Here are the points to calculate the centroid for:

 Point2D p0(0,0);
 Point2D p1(0,1);
 Point2D p2(1,0);
 Point2D p3(1,1);

Here is a code template to start coding from!

Press the "fork" button to work on your own copy of the code!

Later in the class, our points will not be two dimensional anymore, but contain different features of our sounds. E.g. it could be 3D: A dimension for the loudness of the bass, one for the mids and one for the treble. In general the resolution of the spectral data will be much higher and thus a point of 128 dimensions or more can be considered.