Solutions to Homework Task 2

Spoiler Alert! Again, accept the challenge and try on your own first! :)

How our classifier works

Until now, we have been looking at points on a 2D plane. We know how to calculate the distance between them and how to find the centroid of a point cloud. Let's call these point clouds classes from now on. With this tool set at hand, we can already code a simple classifier. We could e.g. detect whether any given point (P_new) is closer to the point cloud which we call class_0 or class_1. We can find out, by calculating the distances of P_new to the centroids of the classes c_0 abd c_1 as shown in the picture below. 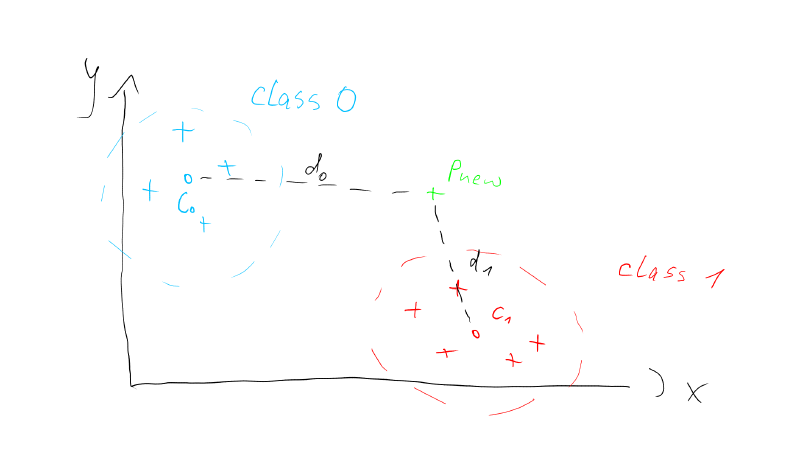In this case the distance d1 is smaller than d0. That would mean our point belongs to class 1 of course.

Why care about points on an X-Y plane?!

Imagine the points are not just drawings on a piece of paper, but actual measurements of real world objects. So instead of giving the axes in the figure arbitrary names like 'X' and 'Y', we can give them meaningful measures of a short sound recording: 'bass' and 'treble'.

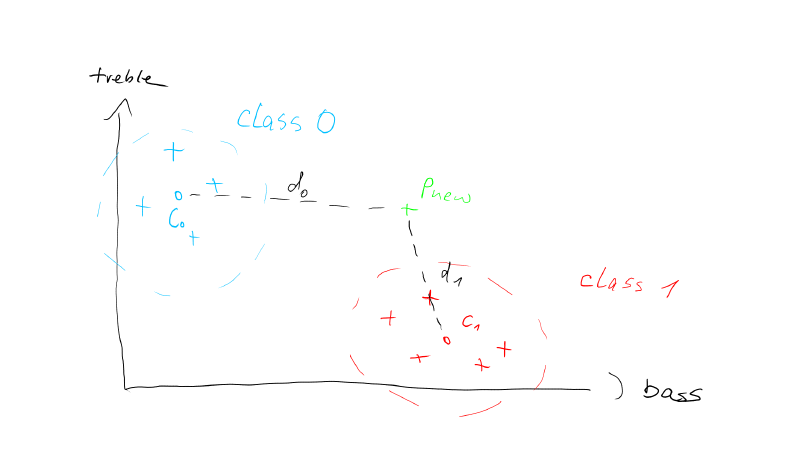
Now we can think of class 1 to represent lower frequency sounds and class 0 to represent sounds containing higher frequencies. Our new point P new basically is a measurement of a new sound that we want to classify. That means we want to know, if it belongs to the low or high frequency sounds.

Note that we can extend this concept easily by taking more measurements of our sounds. For example we could measure how sharp the onsets of our sounds are. A drum sound will have a very sharp onset, whereas a violin sound will have a smooth onset. We call this measurement the 'attack' of a sound. Now let's consider we add the attack as a third dimension to out picture. The axis with the attack will point into the screen.

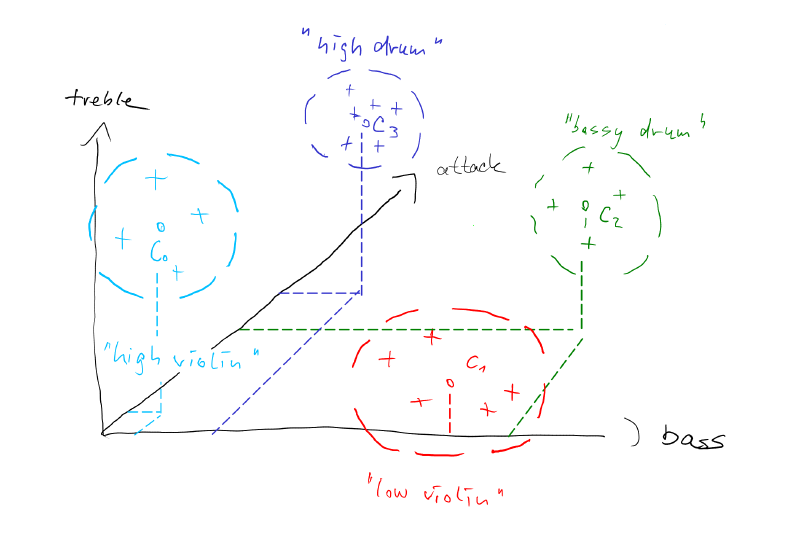
The more attack we have, the sharper the sound. That implies that drum like sounds would be further into the screen and sound with soft onsets, like a soft bowed violin will be closer to us. Not that adding just this one dimension enables us to discern a much greater variety of sounds now.

Description of the classifier code

To be able to successfully classify a new point (a sound), the classifier actually only needs to know the centroid of each class and a way to find the closest centroid to our new point.

As a first step the classifier needs to calculate the centroids. For that it needs to know

all our given points (=measurements of sounds)
and to which class they belong (=classLabels)

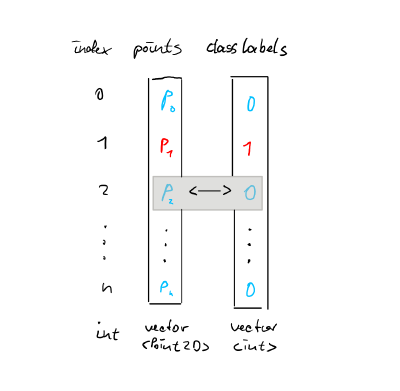
We will feed this data into the classifier via two vectors. The first vector contains all the points and the second one contains the class labels. Note that the indices of the points and class labels should be the same. Such that, when we traverse the vector of points in a for-loop, we can always find out which class it belongs to, by just looking at the same position (index) in the vector with class labels.

vector<Point2D> points = {p0, p1, p2, p3};
vector<int> classLabels = {0, 1, 0, 0};
KMeans classifier = KMeans(points, classLabels, 2);

Our classifier is written in a class called "KMeans" because it most closely resembles a KMeans classifier. So inside the "KMeans.cpp" you will find the guts of our classifier. You can see that, when the KMeans classifier gets instantiated (=the contructor is called), we feed it with the points and the class labels and it immediately calculates the centroids for each class.

KMeans::KMeans(vector<Point2D> &points, vector<int> &labels, int n_classes )
{
    _n_classes = n_classes;
    for(int c=0; c < n_classes; c++) // traverse once for every class
    {
        _centroids.push_back(Point2D(0,0));
        int numPoints = 0;
        
        for(int i=0; i<points.size(); i++)
        {
            if(labels[i]==c) // see if point in points belongs to class c
            {
                _centroids[c] = _centroids[c] + points[i];
                numPoints = numPoints + 1;
            }
        }
        // all points in "points", that belong to the class c are added up
        // now, divide by num of points in class c
        _centroids[c] = _centroids[c]/numPoints;
    }
}

For that it traverses the vector of points a couple of times. Once for every class we have. In each of these traverses it only looks for points of the same class, sums them up, keeps a record of how many they were, and finally divides by the number of points it found. So we end up with the centroid for every class and save it in a vector of centroids called "_centroids". This is a private variable of our class KMeans.

Now, when we classify, we know the centroids and just need to calculate the distance from our new point to every centroid.

int KMeans::classify(Point2D newPoint)
{
    float min_distance = 99238719884798124; // just a biiig distance to start with
    int class_label = -1; // and a wrong class label
    for(int c=0; c<_n_classes ; c++)
    {
        float distance = _centroids[c].getDistance(newPoint);
        if(distance < min_distance)
        {
            min_distance = distance;
            class_label = c;
        }
    }
    return class_label;
}

The idea here is to start with a very large distance and only save a centroid as a candidate if its distance is smaller than the distance we already have recorded. We will automatically arrive at the closest centroid and the minimum distance.

Homework

This week your task will be to modify the code from monday's session to work on n-dimensional data points. "N-dimensional" means the number of dimension can be chosen when we instantiate the clusterer. So the same code should work for 2 dimension (as we programmed it already), 3 dimension, 4 dimensions and so on...

Feel free to fork the repl.it and include a new class "PointND":

Clusterer-2D

The Class PointND should should be structured as shown in the following header file:

#ifndef PointN_H
#define PointN_H
#include <vector>
using namespace std;

class PointND {
    public:
        PointND(int dimensions); // constructor for zero point of n-dimensions

        PointND(vector<float> newND); // constructor for a point which copies the coordinates from an n-dimensional vector

        PointND operator+(PointND& p2);

        PointND operator/(float f);
       
        float getDim(int idx_dimension); // get the component of the indexed dimension, (this was getX() and getY() before)

        int size() // return how many dimension our current point has!
        {
            return _pointND.size();
        }
       
        void print();

        float getDistance(PointND&); // extend the euclidean distance to n dimensions

    private:
        vector<float> _pointND;
};
#endif

Your task is to:

Implement a PointND.cpp file that behaves like our class Point2D on n-dimensional points
Test that class with a 3D distance measurement, and on success
Modify our clusterer to work with the new PointND class!

Have fun and if you're stuck, write a mail, post a message in the forum, or probably its fastest to post on our signal group!

join our signal group!!!

Best wishes, Clemens