Lehrgebiet Mediale Systeme I

WS 2008/09 - Aufgabe 5.4

1. Adjazenzmatrizen
2. Algorithmen für Matrizen der n-ten Dimension
3. Kantenzahl der Topologien (ohne Zentralstation, wenn Topologie dies nicht erfordert)
4. Baumstruktur

1. /\

   Adjazenzmatrizen

   i0-4 = Rechner, i5 = Zentralstation (bei Stern und Rad)

   • Stern

     0	0	0	0	0	1
     0	0	0	0	0	1
     0	0	0	0	0	1
     0	0	0	0	0	1
     0	0	0	0	0	1
     1	1	1	1	1	0

   • Bus

     0	1	1	1	1
     1	0	1	1	1
     1	1	0	1	1
     1	1	1	0	1
     1	1	1	1	0

   • Ring

     0	1	0	0	1
     1	0	1	0	0
     0	1	0	1	0
     0	0	1	0	1
     1	0	0	1	0

   • Rad

     0	1	0	0	1	1
     1	0	1	0	0	1
     0	1	0	1	0	1
     0	0	1	0	1	1
     1	0	0	1	0	1
     1	1	1	1	1	0

   • Binärbaum, i0-6 = Rechner

     0	1	1	0	0	0	0
     1	0	0	1	1	0	0
     1	0	0	0	0	1	1
     0	1	0	0	0	0	0
     0	1	0	0	0	0	0
     0	0	1	0	0	0	0
     0	0	1	0	0	0	0

   • vollständiger Graph

     0	1	1	1	1
     1	0	1	1	1
     1	1	0	1	1
     1	1	1	0	1
     1	1	1	1	0

   • vollständiges Gitter (2D), i0-8 = Rechner

     0	1	0	1	0	0	0	0	0
     1	0	1	0	1	0	0	0	0
     0	1	0	0	0	1	0	0	0
     1	0	0	0	1	0	1	0	0
     0	1	0	1	0	1	0	1	0
     0	0	1	0	1	0	0	0	1
     0	0	0	1	0	0	0	1	0
     0	0	0	0	1	0	1	0	1
     0	0	0	0	0	1	0	1	0

   • Toroid (Torus), i0-8 = Rechner

     0	1	1	1	0	0	1	0	0
     1	0	1	0	1	0	0	1	0
     1	1	0	0	0	1	0	0	1
     1	0	0	0	1	1	1	0	0
     0	1	0	1	0	1	0	1	0
     0	0	1	1	1	0	0	0	1
     1	0	0	1	0	0	0	1	1
     0	1	0	0	1	0	1	0	1
     0	0	1	0	0	1	1	1	0

2. /\

   Algorithmen für Matrizen der n-ten Dimension

   Für alle Ausdrücke gilt, wobei n die Anzahl an Vertices und b bzw. h die Breite bzw. Höhe eines Gitters, gemessen in Vertices, ist:

   Verwendete Integer-Variablen: i, j, c, p, n, b, h for(i = 0; i < n; i++){ for(j = 0; j < n; j++){ c = i – j; p = 0; BEDINGUNG System.out.println(p); } System.out.println(""); } wobei BEDINGUNG stellvertretend steht für: Bus: if( c != 0 ) p = 1; Ring: if( c == 1 | c == -1 | i == n-1 & j == 0| j == n-1 & i == 0) p = 1; Rad: if( c == 1 | c == -1 | i == n-2 & j == 0| j == n-2 & i == 0 | (i == n-1 ^ j == n-1)) p = 1; Vollständiger Graph: if( c != 0) p = 1; Vollständiges Gitter: if( (c == -1 & j%b!=0) | (c == 1 & (j+1)%b!=0) | (c == -b ) | (c == b )) p = 1;

3. /\

   Kantenzahl der Topologien (ohne Zentralstation, wenn Topologie dies nicht erfordert)

   Stern e = v - 1 Bus e = v - 1 Ring e = v Rad (Stern + Ring) e = (2 * v) - 1 Binärbaum e = v - 1 Vollständiger Graph e = v * (v - 1) / 2 Vollständiges Gitter e = (b - 1) * h + (h - 1) * b für b = Breite und h = Höhe des Gitters Quadratisches Gitter e = 2 * (v - sqrt(v)) Toroid e = 2 * b * h für b = Breite und h = Höhe des Toroid-Gitters Quadratischer Toroid e = 2 * v

4. /\

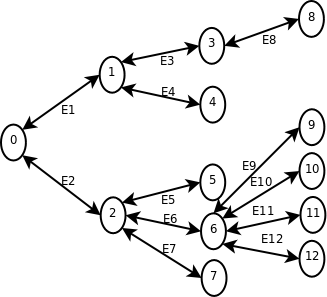
   Baumstruktur

   

   Adjazenzmatrix:

   0	1	1	0	0	0	0	0	0	0	0	0	0
   1	0	0	1	1	0	0	0	0	0	0	0	0
   1	0	0	0	0	1	1	1	0	0	0	0	0
   0	1	0	0	0	0	0	0	1	0	0	0	0
   0	1	0	0	0	0	0	0	0	0	0	0	0
   0	0	1	0	0	0	0	0	0	0	0	0	0
   0	0	1	0	0	0	0	0	0	1	1	1	1
   0	0	1	0	0	0	0	0	0	0	0	0	0
   0	0	0	1	0	0	0	0	0	0	0	0	0
   0	0	0	0	0	0	1	0	0	0	0	0	0
   0	0	0	0	0	0	1	0	0	0	0	0	0
   0	0	0	0	0	0	1	0	0	0	0	0	0
   0	0	0	0	0	0	1	0	0	0	0	0	0

   Inzidenzmatrix:

   V	E01	E02	E03	E04	E05	E06	E07	E08	E09	E10	E11	E12
   0	1	1	0	0	0	0	0	0	0	0	0	0
   1	1	0	1	1	0	0	0	0	0	0	0	0
   2	0	1	0	0	1	1	1	0	0	0	0	0
   3	0	0	1	0	0	0	0	1	0	0	0	0
   4	0	0	0	1	0	0	0	0	0	0	0	0
   5	0	0	0	0	1	0	0	0	0	0	0	0
   6	0	0	0	0	0	1	0	0	1	1	1	1
   7	0	0	0	0	0	0	1	0	0	0	0	0
   8	0	0	0	0	0	0	0	1	0	0	0	0
   9	0	0	0	0	0	0	0	0	1	0	0	0
   10	0	0	0	0	0	0	0	0	0	1	0	0
   11	0	0	0	0	0	0	0	0	0	0	1	0
   12	0	0	0	0	0	0	0	0	0	0	0	1