Differentialgleichung der Schaltung
Diese Aufgabe beschäftigt sich mit der Bearbeitung der folgenden Schaltung:
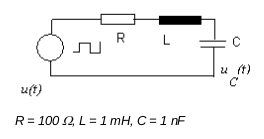
Die zugehörige Differentialgleichung erhält man durch Anwendung des Knoten und des Maschensatzes, wie die folgenden vier Schritte zeigen:
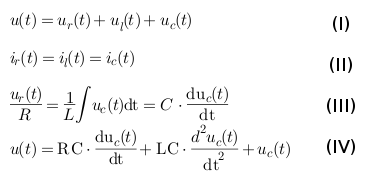
Es handelt sich bei dem Ergebnis um eine Differentialgleichung 2. Ordnung mit konstanten Koeffizienten. Es ist mölich diese mit Hilfe einer Laplace-Transformation zu lösen1.
Durch Umstellung der Gleichung (IV) erhält man:
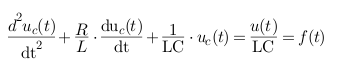
Dies entspricht vom Aufbau der Formel 15.50a aus dem Bronstein (siehe 1). Durch Einsetzen ergibt sich weiterhin:
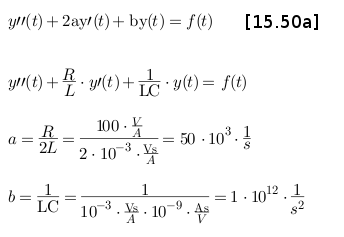
Die weitere Berechnung folgt dem Lösungsweg des Buches.
Rechteckerregung
Schaltungsaufbau in Multisim2:
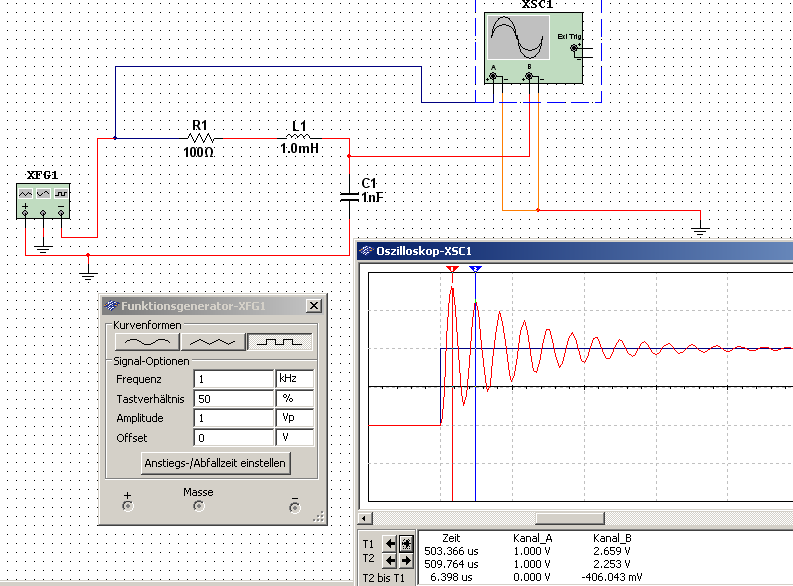
Wie im Fenster des Oszillographen zu sehen hat die Schwingung eine Periode von ungefähr 6,4µs, was einer Frequenz von 156,25 kHz entspricht.
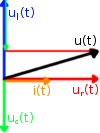
Die Beziehungen der Spannungen lassen sich gut mit Hilfe eines Zeigerdiagrammes veranschaulichen, wenn von einer Sinusförmigen Erregung ausgegangen wird. Die Winkel zwischen den Vektoren geben die Phasenverschiebung der einzelnen komplexen Spannungen wieder. Uc und Ul sind dabei abhängig von der Frequenz. Eine höhere Frequenz vergrößert den Betrag von Ur und verkleinert den von Uc. Ist der kapazitive Widerstand größer als der induktive, so ergibt sich zum Beispiel das nebenstehende Bild:
Sinuserregung
Es folgt eine genauerer Untersuchung verschiedener Frequenzen für Sinusschwingungen mit Multisim. Beispielhaft sollen hier drei Screenshots gezeigt werden:
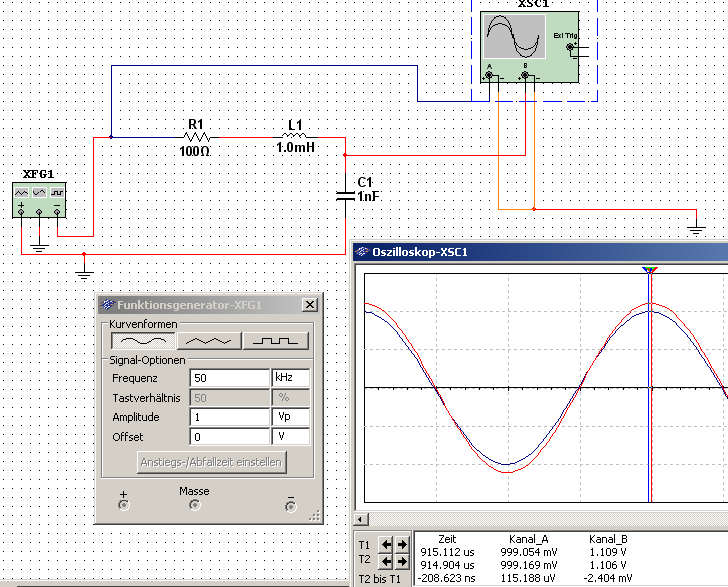
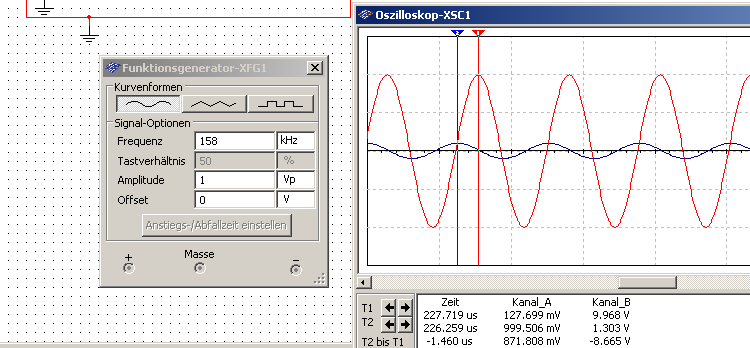
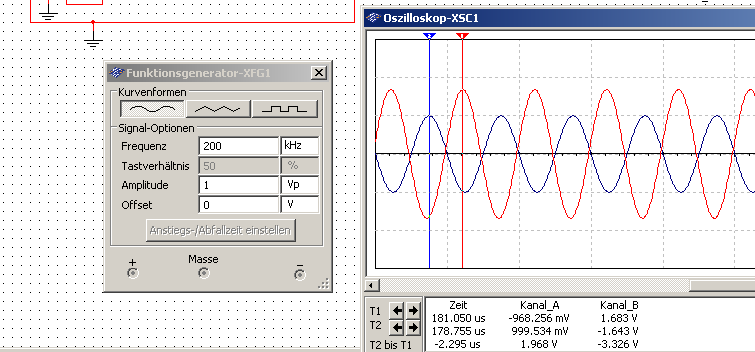
Mit den gesammelten Daten konnten die folgenden Graphen erzeugt werden3:
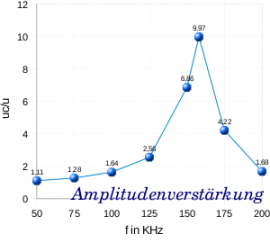
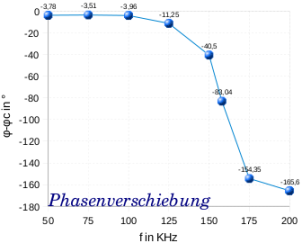
Die Resonanzfrequenz befindet sich, wie zu oben sehen, bei circa 158kHz. Die Phasenverschiebung beträgt hier ca. 83° und die Resonanzüberhöhung ~20dB (ca. das Zehnfache des Ausgangswertes).
Der Bodeplotter
Die Diagramme lassen sich in Multisim auch mit Hilfe eines Bodeplotters gewinnen:
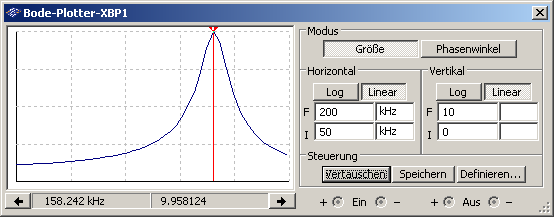
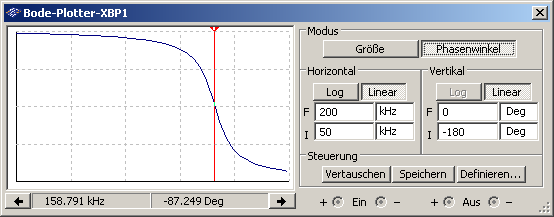
Die oben gewonnenen Ergebnisse der Resonanzfrequenz, des Phasenwinkels und der Verstärkung finden sch hier bestätigt. Der Phasenwinkel befindet sich noch etwas näher an 90°, und bei einer vollständig exakten Bestimmung wird er sich wahrscheinlich noch weiter annähern.
Berechnung
Die Resonanzfrequenz lässt sich allerdings auch genau berechnen. Dazu müssen lediglich die Kapazität und die Induktivität der Schaltung in die folgende Gleichung eingesetzt werden:
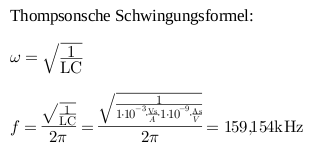
Dieses Ergebnis stimmt mit den vorangegangenen Werten ungefähr überein. Je nach Größe der einzelnen Elemente lässt sich so ein Filter für eine bestimmte Frequenzen bauen, da der Aufbau diese, wie zu sehen, deutlich verstärkt im Vergleich zu anderen Frequenze.