The Traveling Salesman Problem (TSP) is given by the following question: “Given is a list of cities and distances between each pair of cities - what is the shortest route that visits each city and returns to the original city?”
The TSP is an NP-Hard-Problem which does not mean an instance of the problem will be hard to solve. It means, there does not exist an algorithm that produces the best solution in polynomial time. We can not make predictions about how long it might take to find the best solution.
But, we can find a good solution which might not be the best solution. It is ok to find a route amongst 1000 cities that is only few miles longer than the best route. Particularly, if it would take an inordinate amount amount of computing time to get from our good solution to the best solution.
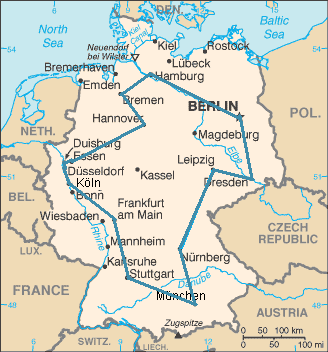
Representation of the Problem¶
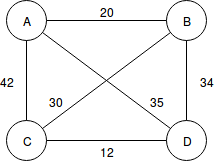A TSP can be modelled as an undirected weighted graph:
- cities = vertices
- paths between cities = edges
- distance of a path = weight of an edge
This graph can be represented as an Adjacency matrix:
| \ | A | B | C | D |
|---|---|---|---|---|
| A | 0 | 20 | 42 | 35 |
| B | 20 | 0 | 30 | 34 |
| C | 42 | 30 | 0 | 12 |
| D | 35 | 34 | 12 | 0 |
But how do we get the distances between cities if we only got the koordinates for each city?
Each city is represented by a cartesian koordinate P
$ P = (p_x, p_y) $
Euclidean Distance¶
Euclidean distance between two points P1 = (x1, y1) and P2 = (x2, y2) is:
$d(P_{1},P_{2}) = \sqrt{(x_{1} - x_{2})^2 + (y_{1} - y_{2})^2}$
from itertools import permutations
def distance(p1, p2):
"""
Returns the Euclidean distance of two points in the Cartesian Plane.
>>> distance([3,4],[0,0])
5.0
"""
return ((p1[0] - p2[0])**2 + (p1[1] - p2[1])**2) ** 0.5
print(distance([3,6],[7,6]))
def total_distance(points):
"""
Returns the length of the path passing throught
all the points in the given order.
>>> total_distance([[1,2],[4,6]])
5.0
>>> total_distance([[3,6],[7,6],[12,6]])
9.0
"""
return sum([distance(point, points[index + 1]) for index, point in enumerate(points[:-1])])
- keep in mind that [:-1] means "all elements if the list without the last"
- enumerate is a function to enumerate all elements of a given sequence
# enumerate example
seasons = ['spring', 'summer', 'fall', 'winter']
print(list(enumerate(seasons)))
def traveling_salesman(points, start = None):
"""
Finds the shortest route to visit all the cities by bruteforce.
Time complexity is O(N!), so never use on long lists.
>>> travelling_salesman([[0,0],[10,0],[6,0]])
([0, 0], [6, 0], [10, 0])
>>> travelling_salesman([[0,0],[6,0],[2,3],[3,7],[0.5,9],[3,5],[9,1]])
([0, 0], [6, 0], [9, 1], [2, 3], [3, 5], [3, 7], [0.5, 9])
"""
if start is None:
start = points[0]
return min([perm for perm in permutations(points) if perm[0] == start], key = total_distance)
keep in mind that the permutation without repitition creates $ \frac{n!}{(n-r)!} $ examples
where n is the amount of elements in the set and r is the number of elements we choose from the set
That means if we have a list of 4 elements we have 24 possible combinations:
$ |perm([a,b,c,d])| = \frac{4!}{(4-4)!} = \frac{4!}{0!} = \frac{4!}{1} = 24 $
# Example for permutations
test_list = ["a", "b", "c", "d"]
test_permutations = permutations(test_list)
for test_perm in test_permutations:
print(test_perm)
- permutations returns tuples with all possible orderings without repeat
- function returns minimum of all possible tuples by the help of the function total_distance from above
import datetime
def main():
points = [
[0, 0],
[1, 5.7],
[2, 3],
[3, 7],
[0.5, 9],
[3, 5],
[9, 1],
[10, 5],
[20, 5],
[12, 12],
[20, 19],
[25, 6],
[23, 7]
]
points = points[:-5]
#points = points[:-4]
#points = points[:-3]
#points = points[:-2]
then = datetime.datetime.now()
result = traveling_salesman(points)
distance_result = total_distance(result)
now = datetime.datetime.now()
print("calculation time", now - then)
print("""
The minimum distance to visit all
of the following points:\n
{0}
starting at
{1} is {2} and takes this
route:
{3}""".format(
points,
points[0],
distance_result,
result))
if __name__ == "__main__":
main()
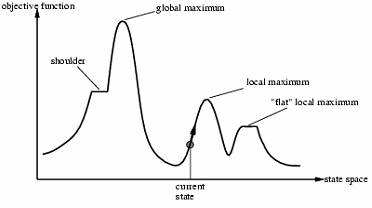
Solving TSP with Hill Climbing¶
Recap: Hill Climbing¶
Idea:
- use only your local solution and evaluate your neighbors to find a better one
- repeat this step until no better neighbor exists
Pros:
- requires few resources (current state and neighbors)
- finds local optimum (global is possible)
- useful if the search space is huge (even unlimited)
Cons:
- is prone to get stuck at the top of local maximum and on plateaus
- strongly depends on “good” initialization
We will use standard Python lists to represent a route through our collection of cities. Each city will simply be assigned to a number from 0 to N-1 where N is the number of cities. Therefore, our list of cities will be a list of uniquie numbers between 0 and N-1
Adjacency Matrix¶
We also need to specify a "distance matrix" that we can use to keep track of distances between cities. To generate a distance matrix for a set of (x,y) coordinates we will use the following function:
def cartesian_matrix(coordinates):
'''
Creates a distance matrix for the city coords using straight line distances
computed by the Euclidean distance of two points in the Cartesian Plane.
'''
matrix = {}
for i, p1 in enumerate(coordinates):
for j, p2 in enumerate(coordinates):
matrix[i,j] = distance(p1,p2)
return matrix
This function takes a list of (x,y) tuples and outputs a dictionary that contains the distance between any pair of cities:
m = cartesian_matrix([(0,0), (1,0), (1,1)])
for k, v in m.items():
print(k, v)
print()
print(m[2,0])
[2,0] gives the distance between the city with number 2 and the city with number 0. In our case the result of [2,0] is the same for [0,2], but for other TSPs this may not be the case (for example if a street between two cities is only one way - we have to take another route)
Read City Coordinates from File¶
def read_coords(file_handle):
coords = []
for line in file_handle:
x,y = line.strip().split(',')
coords.append((float(x), float(y)))
return coords
with open('city100.txt', 'r') as coord_file:
coords = read_coords(coord_file)
matrix = cartesian_matrix(coords)
On real world problems it may be more complicated to generate a distance matrix - you might need to take a map and calculate the real distances between cities.
Compute the Total Distance¶
def tour_length(matrix, tour):
"""Sum up the total length of the tour based on the distance matrix"""
result = 0
num_cities = len(list(tour))
for i in range(num_cities):
j = (i+1) % num_cities
city_i = tour[i]
city_j = tour[j]
result += matrix[city_i, city_j]
return result
Implementing Tweak Operators¶
We will implement the two tweak operators as generator functions that will return all possible versions of a route that can be made in one step of the generator (in a random order).
Generators are iterators which can be only iterated once. They generate values on the fly and do not store them in memory. By using a generator function, we can get each possiblility and perhaps decide to not generate any more variations. This saves the overhead of generating all combinations at once.
import random
def all_pairs(size, shuffle = random.shuffle):
r1 = list(range(size))
r2 = list(range(size))
if shuffle:
shuffle(r1)
shuffle(r2)
for i in r1:
for j in r2:
yield(i,j) # yield is an iterator function
# for each call of the generator it returns the next value in yield
from copy import deepcopy
# Tweak 1
def swapped_cities(tour):
"""
Generator to create all possible variations where two
cities have been swapped
"""
ap = all_pairs(len(tour))
for i,j in ap:
if i < j:
copy = deepcopy(tour)
copy[i], copy[j] = tour[j], tour[i]
yield copy
# Tweak 2
def reversed_sections(tour):
"""
Generator to return all possible variations where the
section between two cities are swapped.
It preserves entire sections of a route,
yet still affects the ordering of multiple cities in one go.
"""
ap = all_pairs(len(tour))
for i,j in ap:
if i != j:
#print("indices from:",i, "to", j)
copy = deepcopy(tour)
if i < j:
copy[i:j+1] = reversed(tour[i:j+1])
else:
copy[i+1:] = reversed(tour[:j])
copy[:j] = reversed(tour[i+1:])
if copy != tour: # not returning same tour
yield copy
# usage
print("start tour swap:",[1,2,3,4])
for tour in swapped_cities([1,2,3,4]):
print(tour)
print()
print("start tour reverse section:",[1,2,3,4])
for tour in reversed_sections([1,2,3,4]):
print(tour)
Getting Started with Hill Climbing¶
To start with Hill Climbing, we need two functions:
- init function that returns a random solution
- objective function that tells us how "good" a solution is
For the TSP, an init function will just return a tour of correct length that has cities aranged in random order.
The objective function will return the length of a tour.
We need to ensure that init function takes no arguments and returns a tour of the correct length and the objective function takes one argument (the solution tour) and returns its length.
Assume we have the city coordinates in a variable coords and our distance matrix in matrix, we can define the objective function and init function by using init_random_tour:
def init_random_tour(tour_length):
tour = list(range(tour_length))
random.shuffle(list(tour))
return tour
init_function = lambda: init_random_tour(len(coords))
objective_function = lambda tour: tour_length(matrix, tour)
Short Explanation of Lambda Functions¶
is the creation of an anonymous function
- lambda definition does not include a return statement
- it always contains an expression which is returned
- you can put a lambda definition anywhere a function is expected
- you don't have to assign it to a variable
# normal function definition
def f(x): return x**2
# lambda function definition
g = lambda x: x**2
print(f(5))
print(g(5))
Basic Hill Climbing¶
def hc(init_function, move_operator, objective_function, max_evaluations):
'''
Hillclimb until either max_evaluations is
reached or we are at a local optima.
'''
best = init_function()
best_score = objective_function(best)
num_evaluations = 1
while num_evaluations < max_evaluations:
# move around the current position
move_made = False
for next in move_operator(best):
if num_evaluations >= max_evaluations:
break
next_score = objective_function(next)
num_evaluations += 1
if next_score < best_score:
best = next
best_score = next_score
move_made = True
break # depth first search
if not move_made:
break # couldn't find better move - must be a local max
return (num_evaluations, best_score, best)
from PIL import Image, ImageDraw, ImageFont
def write_tour_to_img(coords, tour, title, img_file):
padding = 20
# shift all coords in a bit
coords = [(x+padding,y+padding) for (x,y) in coords]
maxx, maxy = 0,0
for x,y in coords:
maxx = max(x,maxx)
maxy = max(y,maxy)
maxx += padding
maxy += padding
img = Image.new("RGB",(int(maxx), int(maxy)), color=(255,255,255))
font=ImageFont.load_default()
d=ImageDraw.Draw(img);
num_cities = len(tour)
for i in range(num_cities):
j = (i+1) % num_cities
city_i = tour[i]
city_j = tour[j]
x1,y1 = coords[city_i]
x2,y2 = coords[city_j]
d.line((int(x1), int(y1), int(x2), int(y2)), fill=(0,0,0))
d.text((int(x1)+7, int(y1)-5), str(i), font=font, fill=(32,32,32))
for x,y in coords:
x,y = int(x), int(y)
d.ellipse((x-5, y-5, x+5, y+5), outline=(0,0,0), fill=(196,196,196))
d.text((1,1), title, font=font, fill=(0,0,0))
del d
img.save(img_file, "PNG")
def reload_image_for_jupyter(filename):
# pick a random integer with 1 in 2 billion chance of getting the same
# integer twice
import random
__counter__ = random.randint(0,2e9)
# now use IPython's rich display to display the html image with the
# new argument
from IPython.display import HTML, display
display(HTML('<img src="./'+filename+'?%d" alt="Schema of adaptive filter" height="100">' % __counter__))
def do_hc_evaluations(evaluations , move_operator = swapped_cities):
max_evaluations = evaluations
then = datetime.datetime.now()
num_evaluations, best_score, best = hc(init_function, move_operator, objective_function, max_evaluations)
now = datetime.datetime.now()
print("computation time ", now - then)
print("best score:", best_score)
print("best route:", best)
filename = "test"+str(max_evaluations)+".PNG"
write_tour_to_img(coords, best, filename, open(filename, "ab"))
reload_image_for_jupyter(filename)
move_operator = swapped_cities
#move_operator = reversed_sections
max_evaluations = 500
do_hc_evaluations(max_evaluations,move_operator)
move_operator = swapped_cities
#move_operator = reversed_sections
max_evaluations = 5000
do_hc_evaluations(max_evaluations,move_operator)
#move_operator = swapped_cities
move_operator = reversed_sections
max_evaluations = 50000
do_hc_evaluations(max_evaluations,move_operator)
